一、什么是堆

堆，是完全二叉树，被称为优先级队列。

分最大堆和最小堆，最大堆中任意节点的值大于或等于它的左、右子节点值，最小堆中任意节点的值小于或等于它的左、右子节点值。

这种数据结构的插入和删除操作，都需要o(lgn)的时间复杂度，但是取最大值和最小值的复杂度为o(1).

堆一般采用数组来存在，满足如下规则：

若堆存储在数组 arr中，当前元素的索引为i，那么

    1.左子节点为 2*i+1

    2.右子节点为 2*i+2

    2.父节点为 (i-1)/2 向下取整

    3.arr中0~arr.length/2-1 为非叶子节点，arr.length/2-1  ~ arr.length为叶子节点

因为堆是完全二叉树，故满足以下特性

n0: 度为0，即为叶子节点数量

n1: 度为1，即为只有左子树或者右子树的节点数量，但完全二叉树，度为1节点，只能是只有左子树。

n2:度为2，即有左右节点的节点数量

n0 = n2 + 1

叶子节点为 n/2 向上取整，或者(n+1)/2 向下取整

二、如何构建堆

构建最大堆

func MaxHeap(data []int) []int  {
   if len(data) < 2 {
      return  data
   }

   // 从 (n+1)/2个位置开始
   curIndex := (len(data) + 1) / 2 -1
   for i := curIndex ; i>=0; i-- {
      jumpMaxHeap(data, i)
   }

   return nil
}

func jumpMaxHeap(data []int, index int)  {
   leftIndex := 2*index + 1
   rightIndex := 2*index + 2

   // 无子节点，不需要处理
   if leftIndex >= len(data) {
      return
   }

   // 无右子节点，进行需要比较 左子节点
   if rightIndex >= len(data) {
      if data[leftIndex] <= data[index] {
         return
      }

      // 交换
      data[leftIndex], data[index] = data[index], data[leftIndex]

      // 递归 判断
      jumpMaxHeap(data, leftIndex)
      return
   }

   // 从leftIndex，rightIndex，index中找出最大值，作为根元素

   if data[index] >= data[leftIndex] && data[index] >= data[rightIndex] {
      // 根节点已是最大值，不需要处理
      return
   }

   if data[leftIndex] > data[index] && data[leftIndex] >= data[rightIndex] {
      // 左子节点已是最大值，和跟节点交换
      // 交换
      data[leftIndex], data[index] = data[index], data[leftIndex]

      // 递归 判断
      jumpMaxHeap(data, leftIndex)
      return
   }

   if data[rightIndex] > data[index] && data[rightIndex] > data[leftIndex] {
      // 右子节点已是最大值，和跟节点交换
      // 交换
      data[rightIndex], data[index] = data[index], data[rightIndex]

      // 递归 判断
      jumpMaxHeap(data, rightIndex)
      return
   }
}

以数组[1,3,5,7,4,6]图解如下：

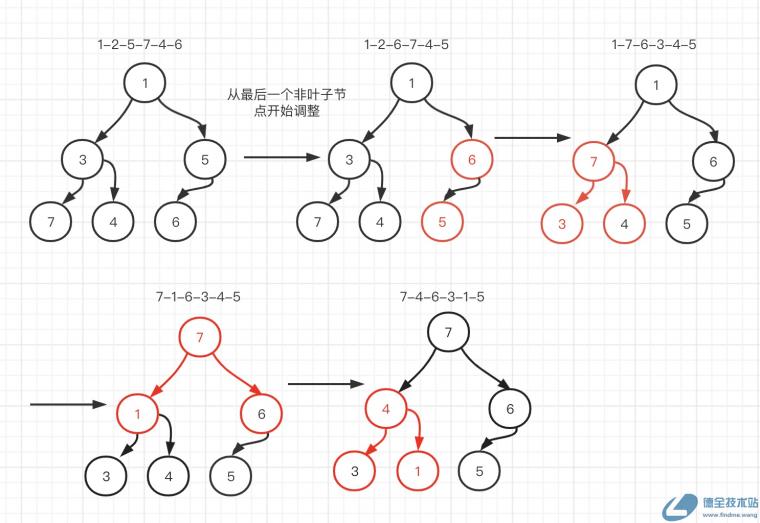
二、堆排序

func heapSort(data []int)  {
   // 1. 构建最大堆
   MaxHeap(data)

   // index 代表已经排序了多少个元素
   // 已经排序的元素，防止最最后的位置
   for index := 0; index < len(data);  index ++ {
      // 将最大堆的，堆顶元素，防止到最后位置
      lastIndex := len(data) - index -1

      data[lastIndex], data[0] = data[0], data[lastIndex]

      // 重新排序堆(0~n-index)个节点
      leftHeap := data[:len(data) - index - 1]
      jumpMaxHeap(leftHeap, 0)
   }
}